Reprinted from Models of brain function Ed. Rodney M. J. Cotterill
© Cambridge University Press, 1989 Printed in Great Britain

Neural Geometry: Towards a Fractal Model of Neurons

A.J. PELLIONISZ

New York University Medical Center

1. GEOMETRIZATION OF BRAIN THEORY

The purposefully "controversial" and therefore long overdue geometrization of brain theory (cf. Pellionisz 1987a,b, 1988a,b, 1989a,b,c) receives major impetus once one can break away from what we were indoctrinated to hold as "Geometry"-that of the uncontroversial Euclidean space. The utterly simple structure of E.g. a physical "space" spun by an x,y,z orthogonal Cartesian reference frame would certainly do for such mundane tasks as parceling one's backyard. One does not have to be a "neurophilosopher" (c.f. Churchland, 1986) to admit, however, that the orthodox Euclidean geometry is not necessarily adequate for a modern geometrical interpretation of structurofunctional properties of some more sophisticated mammalian brains.

1.1. Metric Tensors Say it All ?

An axiomatic shift from extrinsic orthogonal Cartesian frames to intrinsic generalized (nonorthogonal, overcomplete) coordinate systems is well documented in the field'of gaze transformations by neural networks (E.g. from covariant vestibular sensory coordinates to contravariant neck-motor coordinates, via the cerebellar metric tensor; cf. Pellionisz and Peterson 1988, Peterson et al. 1989). Such metrics express an obviously non-Euclidean geometry (see non-zero off-diagonals in the 30-dimensional metric tensor of neck-motor space; ibid). Moreover, since such metric tensors are position-dependent, even rudimentary sensorimotor functional manifolds are shown to represent curved multidimensional hyperspaces. But these are at least still metrical spaces. Are non-metrical neural geometries totally excluded?

Not at all. As it often happens in the history of science, an initial seemingly subtle switch in the basic axioms can leadresearch further and further away from the orthodox direction along which a "taken for granted" rail of thought would blindly take us. The purpose of this paper is to show that single neurons, closely viewed, reveal a dendritic arbor reflecting a grossly non-metrical fractal neural geometry.

1.2. Geometrization of Single Cell Models: Reduction or Conservation of Complexity ?

A close look at single nerve cells is warranted not merely by the anatomical beauty of dendritic arbors which keeps mesmerizing generations of morphologists since Cajal (1911). Indeed, no scientist with true respect of anatomical wonders of nature would dare to consider all nerve cells the same! A fresh look at individual neurons is also long overdue because it is becoming

painfully evident that there is a lack of a single unit model that would both encompass complex physiological (membrane), anatomical (dendritic) properties as well as identify a well-defined computational function, and at the same time could be used as units in neuronal network models. Yet a realistic single cell model, that could also be integrated into neural nets, is vital for the rapidly emerging field of neurocomputing!

1.3. Reduction to Algebra

The venerable McCulloch-Pitts neuron model (1943), while still in use for the meager choice of alternatives, falls short of the above goals from three serious points of view. One is an almost complete disregard of single cell morphology. Neural shape and form is considered irrelevant. All neurons (with a variable n input lines) are essentially equivalent. Electrical phenomena on dendritic trees are left untreated. A second set of problems (in part since this pioneering model was contrived before the dominance of electrophysiology) is the complete ignorance of membrane phenomenology. The "all or none" square pulse of a "flip-flop" disregards those complex ionic mechanisms (approximated by the classical Hodgkin-Huxley equations as early as in 1952) that produce intricate depolarization-curves, giving rise to spikes with various shapes and forxns. Third, the McCulloch-Pitts neuron identified the intrinsic mathematics of neural nets as algebra (as opposed to geometry). Specifically, the computational understructure of the function of neural nets was squarely equated with Boolean algebra (Turing 1948); the mathematical language of serial (von-Neumann) computers. Thus, McCulloch-Pitts neurons (1943), together with the "Hebb-rule" (1949) of the modification of their synaptic efficacies, are still the "nuts and bolts" of building brain-like machines. No wonder that they often turn out as mere variations, multiplexed versions of von-Neumann computers! This is in spite of the fact that the diametrically opposite conceptual foundations of algebraic serial computers and geometrical massively parallel brains were clearly discerned a generation ago (von Neumann, 1958).

It is not that there were no heroic contributions to the geometrization of single neuron models. There were at least two most outstanding endeavors that incorporated the phenomenology of both of the geometrical properties of dendritic trees and electrophysiological properties of neurons (that are in part determined by dendritic geometry). Nonetheless, both seminal contributions left room for further improvement in two aspects; towards extracting abstract computational properties of neurons, and providing a single neuron model that could be practically used in "neural net',' applications.

1.4. Reduction to Closed Analytical Formula, Applied to an Euclidean Shape (Cylinder)

The first memorable attempt was that of Rall (1964). He introduced the brilliant "equivalent cylinder model", an epitome of the Galilean definition of the success in modeling; "unification, simplification, mathematization" (Churchland, 1985). As far as the passive spread of depolarization was concerned, the complex arbor of a dendritic tree could be mathematically equated with simple Euclidean geometrical primitives (cylinders) provided that the bifurcation of the branches followed Rall's "three halves rule"; i.e. that the diameter of the "mother branch" R and those of the "daughter branches" r obeyed the branching power of n=3/2:

Rall's pioneering model ushered in the new era in which dendritic trees were functionally rediscovered. This seminal contribution generated a multitude of quantitative studies concerning electrical phenomena over nerve cell dendritic arborizations (for reviews see Adelman 1971, Cole 1972, Jack at al. 1974, McGregor 1988, Koch and Segev 1988). For at least a decade, the mathematical elegance of a closed analytical formula captivated workers although it was never claimed that the model identified the computational function that single neurons perform in a large neural network. More ominously, evidence started to gather questioning the validity of the very assumptions that were the basis of the mathematical equivalence. First, serious doubts arose if dendritic trees were truly passive, in view of reports claiming that at least on some neurons electroresponsive activity in dendrites can be observed (cf. Koch 1984, Sheperd et al. 1985). Second, "harder" anatomical evidence convincingly documented that the "three halves rule"does not in fact hold for existing neurons. Quantitativecomputerized histology established that the branching power in various neurons of several species (e.g. rats and cats), instead of obeying the theoretical 1.5, ranged up to 2.58 (for cerebellar granule cells), with the lowest branching power being 1.69 (for motoneurons). Specifically, for cerebellar Purkinje cells a branching power of 2.36 was measured (all these data are from Hillman 1979). While an integer branching power of 2 could be justified by the argument of "conservation of dendritic cross section area" that might serve some useful purpose (Hillman 1979), the more typical real values, grossly deviating from 1.5 put severe constraints on the utility of Rall's brilliant equivalent cylinder model.

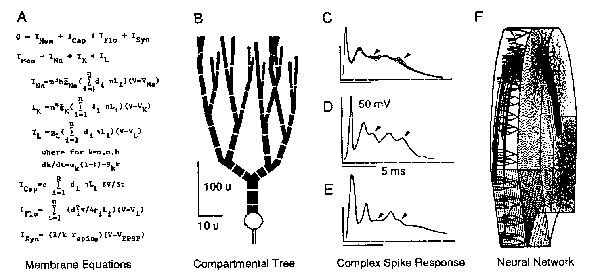
Fig.1 . Levels of Analysis Necessitating Reduction of Complexity (from Pellionisz 1979). A: Hodgkin-Huxley-type membrane equations (1952) that govern electrogenesis in a cylindrical segment. B: Compartmentalization of an ad-hoc Purkinje cell dendritictree. C: Superimposed intracellular recordings of climbing fiber response (CFR) in a cat Purkinje cell, and in the frog (D). E: Computer model (from A-B) explaining the phenomenology of intracellular electrophysiology of CFR. F: Representative neurons from a model of 1.68 million neurons, approximating the neuronal network of the frog cerebellum. Levels of neural complexity are grossly incongruous, unwieldy, and phenomenological.

1.5. Numerical Integration of Nonlinear Differential Equations, Applied to a Compartmentalized Set of Arbitrary Euclidean Shapes

Compartmental models, pioneered by Cooley and Dodge ( 1966) with a wide followership (Jack et al. 1971, Rinzel 1978, Pellionisz 1979, Traub and Llinas 1979, Traub 1982, Koch et al. 1982, Crill and Schwindt 1983, Pongracz 1985, Shelton 1985, Sheperd et al. 1985, Rall and Segev

1988, Koch, Segev 1988 Borg-Graham 1988) directly addressed both problems, plus corroborated membrane equations with single cell morphological and electrophysiological data. The compartmentalization-approach was motivated by electrophysiology of single cells - a majordrive behind neuronal modeling in the sixties and seventies. Those who modelled neurons for a mathematical understanding, leading us to brain-like "neurocomputers", could not even hope for independent support of such useless passion at that time! Quite simply, the enormous data-turnout of that field of research, that has been massively supported for decades, was badly in need of some quantitative synthesis. However, the prevailing trend was to aim towards increasingly finer focus and more and more detailed phenomenological models, leading to an ever-increasing number of free parameters of integrative models. Thus, the state of art in single cell modeling entails literarily thousands of compartments (Shelton 1985), and getting down not only to the level of dendrites (Sheperd at al. 1985), but of dendritic spines (Koch and Poggio, 1983) and individual channels (Crill and Schwindt 1983, cf. Borg-Graham 1988). Modelists, with an eye on synthesis, heroically attempt to close the gap (Rall and Segev 1988).

The compartmental method is based on numerical integration of the updated Hodgkin-Huxley type membrane equations. Therefore, as seen in Fig. 1, spatial compartments of an arbitrarily complex dendritic arbor can bespecified ither as totally passive, or partially or fully active electroresponsive units, and spatial parameters (lengths and branch-diameters) could be freely specified to conform E.g. with any desired "branching power". An obvious advantage of such compartmental single unit modeling is that the phenomenology of complex structuro-functional properties could be approximated to any desired degree of precision. Taking an example from earlier studies of this author; the so-called complex spike response of the Purkinje neuron could be accounted for (compare Fig. 1 CD versus E). The complexity conserved by such models is limited only by the expenditure on computation. Deploying supercomputers, no limit in complexity would be in sight. Nonetheless, such naked "brute force" phenomenology remains both "not complex enough" ; as any compartmental model remains an asymptotic approximation of real dendritic trees, and at the same time "much too complex" since such models based on numerical integration are already grossly inadequate to be synthesized into neuronal networks containing hundreds of thousands of such units (Fig.lF).

There remains therefore a paradoxical need both to reduce the staggering complexity of dendritic trees and to do it in a manner that reduction does not exclude, but in fact would accomplish, a conservation of complexity. Such an approach should retain a flexibility for interpreting a range of real-valued branching powers as well as permit a "mosaic" of various electroresponsive regions over a dendritic tree. This paper argues that the approach of fractal nerve cell modeling initiated here will bring us closer to these hitherto elusive goals.

2. THE FRACTAL MODEL OF NEURAL ARBORIZATION

The plausibility that neuronal arborizations may reflect fractal geometries is substantiated by the fact that arbors of various plants and bushes could already be approximated by fractals. Fractal geometry, although not much older than a decade (the term "fractal" was coined by the "grandfather" of the field, Mandelbrot in 1975), already provided with an array of examples that closed-form codes lead to natural realism in generating geometries (Kawaguchi 1982, Aono and Kunii 1984, Smith 1984 Sullivan 1985, Stanley and Ostrowsky 1986, Barnsley et al. 1988).

Indeed, in his epoch-making book on nature's geometries, Mandelbrot ( 1977) surmised that "it would be nice" if neurons, specifically Purkinje cells of the cerebellum, turned out to be fractals. Nonetheless, this notion was left conjectural - a beautiful challenge to neuroscience.

Beyond physical appearance and a deeply felt "philosophy" that neurons are not Euclidean primitives; spheres and wires, there are three further reasons that compel one to initiate a devoted study of this left-open possibility. Three major principles of the procedure are evidently common in generating neural dendritic trees and fractal arbors. One is the principle of "self-similarity", and the other is the use of recursive algorithms; "code-repetition". Third is the previously mentioned rule of showing a branching power, which appears to reflect a "fractal dimension" of successively reducing, by a real-valued ratio, spatial parameters of increasingly higher-order branches of the dendritic tree.

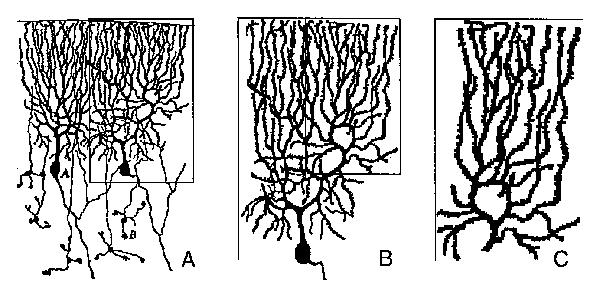
Fig. 2. Self-Similarity. A main principle of fractals, that the whole is similar to its parts, is qualitatively demonstrated for classical Golgi-stained Purkinje cells (from Cajal 1911, Fig.52). Similarity of the arborization of individual cells is shown in A (compare the patterns of two Purkinje cells). A separated Purkinje cell is shown in B, where branchlet of the top right corner is framed. This part magnified (C) displays a qualitative similarity of arborization of the entire neuron (B). Note the limitations and imperfections inherent in using drawings of classic Golgi-stained material.

2.1. Self-Similarity, Code-Repetition and Fractal Dimension

The "self similarity principle" is expounded based on the hypothesis that biological growth follows the mathematical principles of creating a fractal geometry. Growth is based on a repeated access to the genetic code. Thus, for instance, growing two main branches from a trunk of the dendritic tree, and later when in the growing process a tiny twig bifurcates into twiglets, the mother- and daughter branches are characteristically self-similar. This fact may well be based on growth-stages being governed by a recursive process determined by a repeated access to the same "code".

Although quite new, the general methods of fractals and mathematical methods of generating fractal arbors are amply presented in detail in literature (Blanchard 1984, Falconer 1985, Mandelbrot et al. 1985, Amburn et al. 1986). In modeling single neurons, their structural geometry has traditionally been represented by Euclidean shapes (spheres and cylindrical

segments) -just as it is customary to geometrically characterize all man-made objects by such primitives. In contrast, methods of fractal geometry are based on the general principle that if an object is distributed into N parts, each scaled down by a ratio r from the whole, then the dimensionality D can be a real, not just an integer number:

D=logN/log(1/r)

Such a recursive code, generating a hierarchy of elements, each "scaled-down" from the previous by a fractal dimension D, leads precisely to a geometry where the part is very much like to whole. This so-called "self similarity principle" is a strikingly demonstrable feature of dendritic geometry (see Figs. 2 and 4). As shown in Fig.3A by the classic diagram of embryonic Purkinje cells by Cajal (1911), this phenomenon may well be based on growth-stages being governed by a recursive process determined by a repeated access to the same "code".

Fig.3. Fractal Growth Model of Dendritic Arbor by Code Repetition. Top inset A (from Caja11911 , Fig.69) documents that Purkinje cells in embryonic stage ofdevelopment consist of a basic "spatial code". A similar"spatial code" (C) arising from a trunk (B) grows in this fractal model into a realistic dendritic arbor in two further generations (D and E). The fractal arbor is generated in this paper by the so-called "String Re-Writing L-system" originally developed by Lindenmayer, Smith, Prusinkiewicz and Saupe, c.f. Barnsley et al. 1988. This method replaces line segments, in subsequent stages of growth, by the whole "spatial code". The code is shown here in C, to be compared with the "budding" neuron in A above C.

As mentioned, data available in literature (Hillman 1979, before fractals emerged) lend themselves to the interpretation here that Purkinje cell arbors, rather than following Rall's 3/2 rule, conform with a fractal dimension corresponding to the branching power of 2.36. As for the angular pattern of the arborization, the method of iterated function system (referred to as IFS-code) is used (Barnsley et al. 1985, 1988).

Fig. 3. illustrates the use of these procedures on a contemporary graphical workstation for generating a fractal model of a Purkinje cell (cf. Pellionisz 1989a,b). Graphical modeling techniques and methods are in use to investigate and replicate various specific dendritic arbors, most particularly the cerebellar Purkinje cell.

The initial plausibility study (shown in Fig.3, corroborating early stages of fractal growth with

embryonic development of Purkinje cells) encouraged a more detailed analysis of a contemporary graphical renderings of a Purkinje neuron. One of the most recent and best Purkinje cell renderings is found in Tank et al. 1988; displaying a fluorescent calcium-image From guinea pig slice preparation. This neuronal arborization is reproduced from the literature(Figs.4B and 5F).

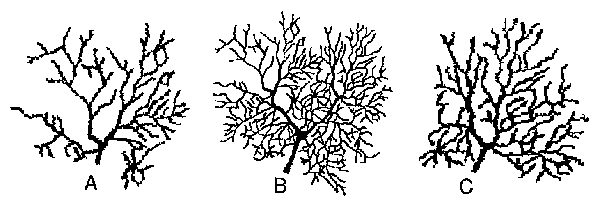
Fig.4. Self-Similarity Demonstrated by a Contemporary Purkinje Cell Rendering: Central inset B displays a guinea pig Purkinje cell (from Tank et al., 1988; fluorescent Ca-recording in a cerebellar slice-preparation). Top left corner of this dendritic arbor is shown (magnified) at left (A), and top right branchlet is displayed in C. Note the qualitative similarity between the whole neuron and its parts.

Self-similarity of (top left and top right) branches of the dendritic tree is qualitatively apparent in Fig.4 (compare B with either A or C). Both the whole dendritic tree and its parts are essentially composed of a main trunk, bifurcating in a Y-shape manner, with subsequent bifurcations mimicking this basic "spatial code". It could be noted that this contemporary high-resolution mapping of a Purkinje cell is much more suitable for anatomical reconstruction than ancient drawings from Golgi-stained material. Accordingly, as illustrated in Fig.S., a surprisingly simple "code" (see inset B in Fig.S) is suitable for producing, in three successive generations, a fractal model of the dendritic tree. The fmal result is shown in Fig.SE, which is qualitatively directly comparable to the real Purkinje cell of the guinea pig (Fig.SF). Beyond the general pattern of arborizations, note the Y-shaped endings of the fractal tree, mimicking similar branchlets of the real Purkinje cell.

A computerized video-display (shown in Pellionisz 1989b) has also been constructed, demonstrating the growth-process of fractal neurons of Figs. 5. and 3.

3. IMPLICATIONS OF FRACTAL NEURAL GEOMETRY

This paper serves the basic purpose of substantiating the "conjecture" of fractal growth of dendritic trees of nerve cells. Fractal models display self-similarity of micro- and macrofeatures of the arbor. It is argued that the bifurcation-rule of branching expresses a fractal dimension, and the model reveals some simple codes responsible for generating dendritic arbors. The road towards developing a full structuro-functional fractal model of neurons is certainly long and-as most geometrizations in natural sciences-probably uphill. Nevertheless, it opens up several possibilities and thus appears well worth pursuing.

The simplest aspect of further progress is that nerve cells other than Purkinje neurons could also be investigated. Indeed, while Purkinje cells display among the most dramatic-looking dendritic

arbor, it is an exceptional simplicity that they are practically flat and thus lend themselves to direct two-dimensional analysis. Although full three-dimensional fractal reconstruction necessitates a generalization of the "String Re-Writing L-Systems" used in this paper, that particular difficulty is only technical and can be overcome with relatively modest effort.

The preliminary fractal reconstruction in Fig.S, however, also flashes out an agenda ranging from immediately possible tasks to more remote but potentially very important endeavors. 3.1. Accelerating Agenda of Geometrization

3:1.1. Quantitative Computerized Histology: Aiming at Fractal Parameters

One of the most direct and eminently feasible implications of the above study is that it provides with a new guidance for existing efforts in quantitative computerized histology (cf. Hillman 1979). One immediate possibility in computerized quantitative histology is the shift from measuring branching powers of dendritic bifurcations towards establishing the fractal dimension in a large enough anatomical sample of various neurons. In a more global sense, facing any geometry (including that of neurons) one of the most important search is directed towards disceming its invariants. Remember the notion by one of the most significant geometer of all times, Felix Klein (1939): that "geometry is the theory of invariants"! By comparing Fig. 5B and E it is clear that the "spatial invariants" of the tree are encapsulated in the simple "code" in Fig.5B. Actual measurements of the very few quantitative parameters on a sufficiently large sample of Purkinje neurons could conclude in such a "seed" of the "Platonic Purkinje cell", and similarly in "seeds" of other types of neurons. In addition to the volume of such research projects requiring computerized quantitative anatomy, a sizable effort is necessary to elaborate the present preliminary fractal model (which is hitherto totally deterministic) towards a biologically more realistic stochastic theory of "random" fractals (Mandelbrot 1977).

3.1.2. Neural Modeling: Reduction and Conservation of Complexity by Fractals

As outlined in the introduction of this paper, an important motive behind fractal neural models is their capacity to both reduce complexity and at the same time conserve the full richness of the structure of the arbor. It is noteworthy that a similar reduction and conservation is attained by the genome; this is why the "code" (cf. Fig.SB) is also called"seed" in this paper. It is evident, that at this preliminary stage of fractal modeling, the encapsulation of neural complexity has been demonstrated in this paper only in a structural sense. But various types of neurons are built differently not for reasons of anatomy but their function. Thus, the hypothesis here is that a "shape-code" of a specific class of neurons is probably highly influential on the electrophysiological properties of that type of neuron. Also, since nature evidently developed a morphological "self similarity" of micro- and macro domains, there is a reasonable likelihood that a "self similarity" may show up in electrophysiological properties of micro- and macro domains of neurons. One is prepared to follow up these functional implications by applying a systematic analysis (with the use of the proven compartmental modeling technique) to fractal "seeds" versus various 1-5 generation arbors. While it is difficult to exactly foresee all implications of such enormous reduction/conservation at this outset, it is a distinct possibility that a hypothetical "spatial code" of the distribution of electroresponsive areas over a dendritic tree, if confumed, could lead to a structuro-functional single unif model that encapsulates essential

functional geometrical properties of the particular neuron-type. Another likely implication is :hat the classical Hebb-rule (that hypothesized synaptic efficacy-changes over the whole iendritic tree as a function of the single scalar of output firing of neuron) could be "dimension~lly upgraded" by the use of the fractal model such that the scalar becomes a neuron-specific-activity-matrix, over the whole tree. Such a matrix, in fact the functional expression of dendritic geometry, would determine the built-in learning propensities of the specific neuron.

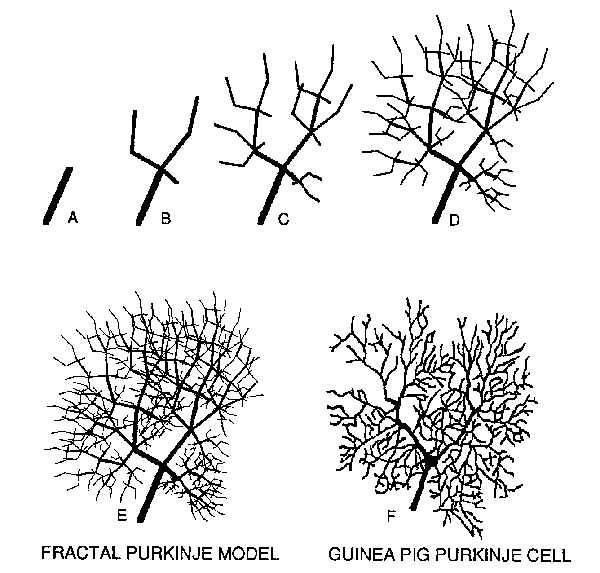
Fig.5. Demonstration of the Feasibility of Fractal Models to Reduce and at the Same Time to Conserve Complex Arborizations. A-D show an initial trunk and three subsequent stages of fractal growth of an arbor, using the "spatial code" displayed in B. Comparison of B and C well illustrates the "string re-writing L-system technique"; dendritic branches replaced by a fractally proportioned whole "code". The fourth-generation fractal tree is shown in E, which is to be compared with the real guinea-pig Purkinje cell dendritic arborization shown in F (same cell as in Fig.4).

3.1.3. Neural Growth: Structural Manifestation of Repeated Access to Genetic Code

One of the most basic, but in all likelihood rather remote, implication of the emerging fractal neural modeling is that it corroborates a spatial "code-repetition" of the growth process with the repetitive access to genetic code. This conceptual link between the two meta-geometries of double helix and "fractal seed" may ultimately lead to precisely pinpointing those exact differences in the "genetic" code that lead to a differentiation to Purkinje-, pyramidal cell, Golgi-cell or other type of specific neurons. It must be emphasized, however, that establishing a rigorous

relation of these "code sequences" to the genetic code that underlies the morphogenesis of differentiated neurons may be far in the future. So is the use of any eventually established "recursive code" to generate semiconductor-based electronic neuromimes, E.g. by manipulating diffusion-properties according to such codes. These ultimate problems of fractal growth are enormously complicated by such facts that E.g. the emerging structural elements (either in biological or non-living medium) are not independent of one another the growth of neighboring dendritic branches may seriously affect one another through the extracellular milieu.

3.2. A Broadening Perspective of Neural Geometry

Raising sights above Euclidean spaces it is apparent that metrical properties of (quasi)linear, derivable multidimensional manifolds (e.g. those governing gaze; Pellionisz 1988a ) are but the simplest features of neural geometry. Upon very close examination a fractal understructre emerges. At the other end of the spectrum it is also known that if large neural networks revert to a nonlinear and non-metrical domain then strange attractors may emerge, revealing (for instance, in EEG) a chaotic geometry (Guevara et al. 1983, Chay 1984, Skarda and Freeman 1987). Regrettably, the relation of fractal, metrical and chaotic neural geometries is quite obscure at the moment. Fractal growth can be related to (quasi)linear metrical network transformations and chaotic nonlinear dynamics mostly in terms of mathematics or (worse) of philosophy as yet. Mathematically, transient emergence of non-linear dynamics from a linear domain is well documented, and can be easily demonstrated in physical examples (see transition of laminar flow to turbulence or the transition of a regularly "dripping faucet" into the domain of irregularity; developing a chaotic attractor). Likewise, connection of fractal geometries with chaos is vigorously researched, revealing for instance fractal-like "self-similarity" of the whole chaotic attractor with its parts (c.f. Henon 1976 or Barnsley et al. 1988).

Finally, in terms of philosophy, one may find it remarkable that chaotic, metrical and fractal neural geometries of the macro-, medium- and micro-domains of the CNS appear to be in a difficult relationship. After all, the external world that the brain reflects is laden with a similar problem. Newtonian mechanics, that applies to the medium-domain, is "hopelessly" complicated by "controversial" relativistic- and quantum-mechanics. They are is still a must if one strives to, be a creative scientist; e.g. cosmologist of the macro-world, or particle physicist of the microcosmos - or just wants to avoid being stuck at the mediocre level of an uncontroversial car mechanic.

Acknowledgement: This preliminary study has been conducted in the framework of grant application "Neural Geometry" to NIMH Program "Mathematical/Computational/Theoretical Neuroscience".

References

Adelman WJ (1971) Biophysics and physiology of excitable membranes. Van Nostrand Reinhold, NY

Ambum P, Grant E, Whitted T (1986) Managing geometric complexity with enhanced procedural methods. Comp. Graphics

Aono M, Kunii TL (1984) Botanical tree image generation. IEEE Comp. Graphics & Appl. 10-33

Barnsley MF, Demko S (1985) Iterated function systems & the global construction of fractals. Proc. Royal Soc. I,ond. A399, 243-275

Barnsley MF, Devaney RL, Mandelbrot BB, Peitgen HO, Saupe D, Voss RF (1988) The science of fractal images. Springer, Berlin

Blanchard P (1984) Complex analytic dynamics on the Riemann sphere. Bull. Amer. Math. Soc. 11: 85-141

Borg-Graham LJ (1988) Modeling the electrical behavior of cortical neurons - simulation of hippocampal pyramidal cells. In: Comp. sim. in brain science (Ed. RMJ Cotterill), Cambridge U.Press, pp. 384-404

Cajal R (1911) Histologie du systéme nerveux de 1'homme et des vertébrés. 2 Volumes, Paris, Maloine

Chay TR (1984) Abnormal discharges & chaos in a neural model system. Biol. Cybem. 50, 301-311

Churchand, PS. (1985) Neurophilosophy: Towards a UnifiedUnderstanding of theMind-Brain. MIT'Press, Boston MA

Cole KS (1972) Membranes, ions and impulses. Univ. Calif. Press

Cooley J, Dodge FA (1966) Digital computer solutions for excitation and propagation of the nerve impulse. Biophys. J. 6: 583-599

Crill WE, Schwindt PC (1983) Active currents in mammalian central neurons. Trends Neurosci. 6: 236-240. Falconer KJ (1985) The geometry of fractal sets. Cambridge Univ. Press.

Guevara MR, Glass L, Mackey MC, Shrier A (1983) Chaos in neurobiology. IEEE Trans. Systm.Man.Cybernet. 13:790-798.

Hebb DO (1949) The organization of behaviour. John Wiley, NY

Hénon M (1976) A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 50:69-77

Hillman D (1979) Neuronal shape perameters and substructures as a basis of neuronal form. In: The neurosciences. IVth study program. FO Schmitt and FG Worden (eds) MTT Pess, Boston pp. 477-498

Hodgkin AL, Huxley AF (1952) A quantitative description of membrane current & its application to conduction & excitation in nerve. J. Physiol. 117:500-S44.

Jack JJB Redman SJ (1971) An electrical description of the motoneurone & its application to the analysis of synaptic potential. J. Physiol. (L.ondon), 215:321-352.

Jack JJB, Noble D, Tsien RW (1975) Electric current flow in excitable cells. Clarendon Press, Oxford Kawaguchi Y (1982) A morphological study of the form of nature. Comp. Graphics.

Klein F (1939) Elementary Mathematics form an Advanced Viewpoint, Dover, NY.

Koch C (1984) Cable theory in neurons, with active, linearized membranes. Biol. Cyb. 50, 15-33

Koch C, Poggio T, Torre V (1982) Retinal ganglion cells: a functional interpretation of dendr. morphology. Phil. Trans. R. Soc. Concl. B. 298: 227-264

Koch C, Poggio TA (1983) Electrical properties of dendritic spines. Trends Neurosci. 6: 80-83 Koch C, Segev I (1988) Methods in neural modeling. MIT Press

Mandelbrot BB, Gefen Y, Aharony A, Peyriere J (1985) Fractals, their transfer matrices and their eigendimensional sequences. J. Phys. A. 18:335-354

Mandelbrot BB (1977) The fractal geometry of nature, W.H. Freeman, New York

McCulloch WS, Pitts W (1943) A logical calculus of the ideas immanent in nervous activity. Bulletin of Math. Biophys, 5, 115-133.

McGregor RJ (1988) Neural & brain modeling. Academic Press

Pellionisz AJ (1979) Modeling of neurons & neural networks. In: The Neurosciences: IV Study Program (eds: Schmitt FO & Worden FGB) MTTG Press, Boston, MA, pp. 525-546

Pellionisz A (1987a) Tensor network theory of the central nervous system. Encyclopedia of Neuroscience , ed. G. Adelman, Boston: Birkhauser

Pellionisz A (1987b) Tensor geometry as the mathematical language of neural networks. Brain theory foundation for neurobotics and neurocomputers. Proc. of IBRO II.World Congress, Neurosci, Suppl. to Vol 22, p. S 101

Pellionisz AJ (1988a) Vistas from tensor network theory: A horizon from reductionalist neurophilosophy to the geometry of multi-unit recordings. In: Computer simuhition in brain science. Cotterill R (eds) Univ. Press, Cambridge pp 44-73

Pellionisz AJ (1988b) Tensor geometry: A language of brains & neurocomputers. Generalized coordinates in Neuroscience & robotics, In: Neural computers (Proc. of the NATO Adv. Res. Workshop) Eckkmiller R & Malsburg Ch(eds) Springer,Berlin381-391

Pellionisz AJ ( 1989a) Neural geometry: Tensor network theory of the CNS. Monograph, Cambridge University Press (in preparation)

Pellionisz AJ (1989b) Neural geometry: The need of researching association of covariant and contravariant coordinates that organizes a cognitive space by relating multisensory-multimotor representation. Proc. of the International Joint Conference on Neural Networks, Washington D.C.

Pellionisz AJ (1989c) Fractal geometry of Purkinje neurons: Relationships among metrical and non-metrical neural geometries. Soc. Neurosci. Abst. (In Press)

Pellionisz AJ, Peterson BW (1988a) A tensorial model of neck motor activation. In: Control of head movement Peterson BW , Richmond F (eds) Oxfotd Univ. Press pp 178-186

Peterson BW, Pellionisz AJ, Baker JF, Keshner E (1989) Functional morphology and neural control of neck muscles in mammals. Amer. Zool. 29:139-149

Poggio T, Torre V, Koch C, (1985) Computational vision & regularization theory, Nature, Vol. 317, No. 6035 Pongracz F (1985) The function of of dendritic spines: A theoretical study. Neurosci. 15: 933-946 Prusinkiewicz, P (1986) Graphical applications of L-systems. Proc. of Graphics. Vision Interface 247-253.

Rall W (1964) Theoretical significance of dendritic trees for neural input-output relations. In: Neural Theory & Modeling, R.F.Reiss, ed. Stanford, CA: Stanford Univ. Press, pp.73-97.

Rall W, Segev I ( 1988) Excitable dendritic spine clusters: nonlinear synaptic processing. In: Computer simulation in brain science. Ed. Cotterill RMJ, Cambridge Univ. Press. pp. 26-43

Rinzel J (1978) Integration & propagation of neuroelectric signals. In: Studies in math. biology. (S.A. Levin, ed), pp. 1-66. Math. Assoc. Am. Washington, DC

Shannon C (1948) A mathematical theory of communication. Bell System Technology J. 27, 3-4.

Shelton DP (1985) Membrane resistivity estimated for the Purkinje neuron by means of a passive Comp. model. Neurosci. 14, 111-131.

Sheperd GM, Brayton RK, Miller JP, Segev I, Rinzel J, Rall W (1985) Signal enhancement in distal cortical dendrites by means of interactions between active dendr. spines. Proc. NaH. Acad. Sci. USA 82;2192-2195

Skarda CA, Freeman WJ (1987) How brains make chaos in order to make sense of the world. Brain Behaviorat Sciences vol. 10. pp. 161-195.

Smith AR (1984) Plants, fractals & formal languages. Comp. Graphics, 1-10

Stanley HE, Ostrowsky, N (eds) (1986) On growth & form: Fractal & non-fractal pattems in physics. (Martinus Nijhoff Publishers, Dordrectht, Netherlands)

Sullivan D (1985) Quasiconformal homeomorphism & dynamics I. Ann. Math. 122:401-418

Tank DW, Sugimori M, Connor JA, Llinás R (1988) Spatially resolved Calcium dynamics of mammalian Purkinje cells in cerebellar slice. Science, 242:633-828

Traub R, Llinás R (1979) Hippocampal pyramidal cells: significance of dendritic ionic conductance for neural function & epileptogenesis. J. Neurophys. 42:476-496

Traub RD (1982) Simulation of intrinsic bursting in CA3 hippocampal neurons. Neurosci., 7, 1233-1242 Turing AM (1948) Intelligent machinery. Rect. Natl. Phys. Lab. Teddington

von Neumann J (1958) The computer & the brain. New Haven: Yale Univ. Press